Примена софтверског сата је задатак који се ученицима често даје на часовима информатике. Дакле, наставник је уверен да ученик добро познаје не само програмски језик који се проучава, већ и тригонометрију. Али рачунар на коме студент решава овај проблем је превише моћан за њега, чак и ако је древни 386., да не спомињемо модерне. Уз сву математику која се тамо бави, и Ардуино - тако је одлучио аутор књиге Инструцтаблес под надимком тхеистистистформерликновнасНаегели. Овде је узет 3.3 В Ардуино Про Мини, једнобитни дисплеј за телефон Нокиа 5110, модул сата у реалном времену на чипу ДС3231, батерија и контролер напуњености, различита додатна опрема:
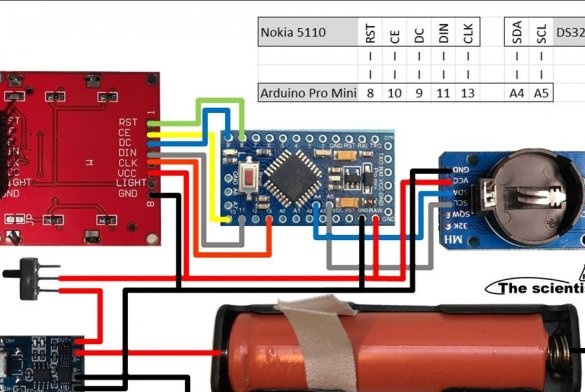
Он све то сакупља по овој шеми:
А ево шта он ради:
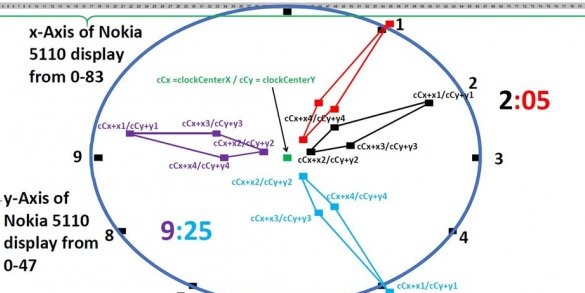
Али у монтажи нема ништа компликовано. Најзанимљивија ствар је математика за коју мајстор то узима. Затим приказује смер координата на дисплеју:
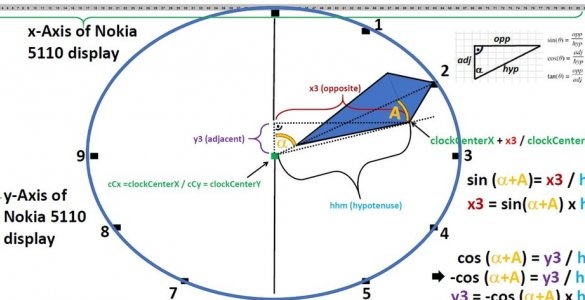
Комплицирајући задатак себи, мајстор имплементира стрелице сложеније од сегмената линија, школарци на часовима информатике ретко дођу до такве компликације, а онда, кад одрасту, надокнађују их.
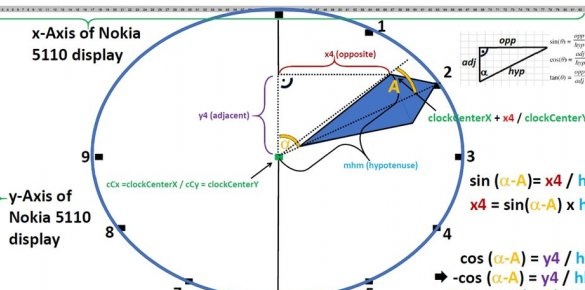
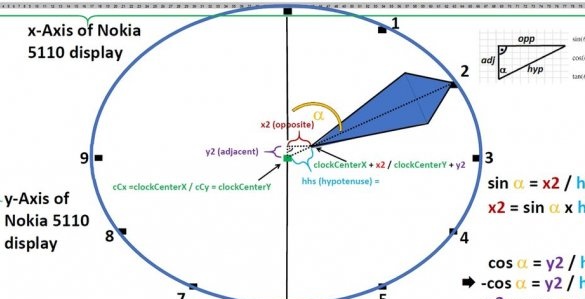
Чаробњак се налази на најсложенијој верзији где се стрелица састоји од четири тачке и приказује формуле за израчунавање координата ових тачака, користећи два пута као пример: 9:25 и 2:05.
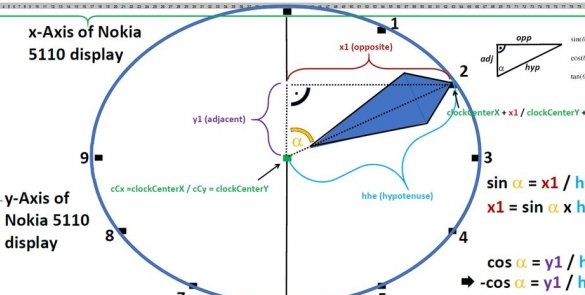
Угао нагиба минутне шаке у степенима је лако израчунати: само множите број минута са 6. Само одложите угао у смеру казаљке на сату, а не против, као што се обично ради. У смеру казаљке на сату, угао је теже израчунати, имајући у виду да не скаче из подела у поделу, већ се глатко помера између њих:
угао = (сати к 30 °) + (минута к 0,5 °)
Па, смер координата на екрану такође треба да се узме у обзир, успут, у школи ДОС БАСИЦ се такође разликује од оне коју користе математичари. Али пошто ће стрелице бити четворокраке, тада је математика лебдета нешто сложеније.
Професионална деформација програмера је моћна ствар, може чак и да натера плажу да особа уместо опушта:
Али сада је скица спремна, мајстор је ставља овде. Након преузимања морате да промените екстензију датотеке из непознате у ино.
Па, пошто понављате конструкцију вероватно нећете поново проћи сву математику, било би лепо уради сам, са сопственом математиком (узимајући у обзир дебљину зида и тако даље), бар случај, на пример, од шперплоче или плексигласа, а не узимајте готове или 3Д штампане.
Сат поновљен од стране Инструцтаблес ресцуесевен: